题解 U534160 【进入 k 进制星球】
题目链接:进入 k 进制星球。
关于题目:作为 T3,一道数学题。
应用算法:数论?
\(\ \ \ \ \ \ \)这道题的题意非常明确,就是求在 \(k\) 进制下 \(n!!\) 的位数。
\(\ \ \ \ \ \ \)前置知识:
双阶乘:双阶乘是一个数学概念,用n!!表示。正整数的双阶乘表示不超过这个正整数且与它有相同奇偶性的所有正整数乘积。——百度百科
对数:在数学中,对数是对求幂的逆运算。——百度百科
\(\ \ \ \ \ \ \)会了对数,自然就可以知道这道题要求的答案就是 \(log_k n!!+1\)。
\(\ \ \ \ \ \ \)看一眼数据范围:
\(\ \ \ \ \ \ \)对于 \(50\%\) 的数据,\(1\leqslant n \leqslant 2\times 10^6\)
\(\ \ \ \ \ \ \)对于 \(100\%\) 的数据,\(1\leqslant n \leqslant 2\times 10^9\),\(10 \leqslant k \leqslant 100\)
\(\ \ \ \ \ \ \)部分分还是给的挺足的,那么我们就先解决前 \(50\%\) 的暴力:
五十分做法:
\(\ \ \ \ \ \ \log_k n!!+1=\sum\log_k i(i=2;i\leqslant n;i=i+2)+1\)
\(\ \ \ \ \ \
\)没错,这就没了。是不是很简单?
\(\ \ \ \ \ \ \)具体处理主要有以下三点:
1、C++ 自带的求对数的函数有两个:
double log(double x)函数返回 \(\ln x\),double log10(double x)函数返回 \(\lg x\)。2、想求 \(\log_kn\),自然就需要换底公式,在这里,我采用以 \(e\) 为底的对数进行中介:
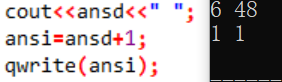
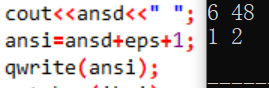
ansd+=log(i)/log(k);。3、在统计答案时,由于前面用的都是浮点数,但是最后需要一个整数,一定要注意精度的问题:
ansi=ansd+eps+1;。eps是很重要的,一定要有,实例如下:
代码(码风不喜勿喷): 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
using namespace std;
int n,k,ansi;
long double ln_k,ansd;
//每个数组或变量的含义详见处理过程。
in int qread()
//快读
{
int x=0,f=1;
char c;
c=getchar();
while(c<'0'||c>'9')
{
if(c=='-')
{
f=-1;
}
c=getchar();
}
while(c>='0'&&c<='9')
{
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
in void qwrite(re int x)
//快写
{
if(x<0)
{
putchar('-');
x=-x;
qwrite(x);
}
else
{
if(x>9)
{
qwrite(x/10);
}
putchar(x%10+'0');
}
}
signed main()
{
n=qread();
k=qread();
//读入
ln_k=log(k);
//ln_k表示以e为底k的对数
for(re int i=2;i<=n;i+=2)
{
ansd+=log(i)/ln_k;
//ansd+=以k为底i的对数
}
ansi=ansd+eps+1;
//统计答案,这个eps真的非常重要
qwrite(ansi);
putchar('\n');
//输出答案
return 0;
}

一百分做法:
\(\ \ \ \ \ \ \)由于 \(1\leqslant n \leqslant 2\times 10^9\),我们继续使用 \(O(n)\) 的算法一定会如上 \(TLE\),那么,我们就需要一个时间复杂度更小的算法。\((O(\sqrt n)?\ \ O(\log n)?)\)
\(\ \ \ \ \ \ \)怎么在低于 \(O(n)\) 的时间复杂度内求得 \(log_kn!!+1\) 呢?对于双阶乘的计算我们不是很熟悉,但是由于题目中规定 \(n\) 为偶数,根据定义,我们可以将双阶乘转化成我们比较熟悉的阶乘和乘方相乘的形式:\(n!!=\dfrac{n}{2}!\times 2^{\dfrac{n}{2}}\),那么要求的答案:\(log_kn!!=log_kn!+\dfrac{n}{2}\times log_k2\)。
\(\ \ \ \ \ \ \)现在问题的关键就在于,怎么在低于 \(O(n)\) 的时间复杂度内求得 \(log_kn!\) 呢?阶乘我们就熟悉了,利用一个神奇的公式:斯特林公式:\(n!\approx \sqrt{2\pi n} \left( \dfrac{n} {e} \right)^n\) 即可。 >\(\ \ \ \ \ \ \)斯特林公式(Stirling's approximation)是一条用来取n的阶乘的近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特林公式十分好用,而且,即使在n很小的时候,斯特林公式的取值已经十分准确。——百度百科
\(\ \ \ \ \ \ \)由于斯特林公式只是一个近似公式,\(n\) 越大时误差越小,那么我们就只用它去处理暴力会时间超限的后 \(50\%\) 的数据点: \(\log_k n!!+1 \approx \log_k \sqrt{\pi n} \left( \dfrac{n} {2e} \right)^n +1+\dfrac{n}{2}\times log_k2=\dfrac{1} {2}\log_k \pi n+n\times \log_k \dfrac{n} {2e}+1+\dfrac{n}{2}\times log_k2\)
代码(码风不喜勿喷): 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
using namespace std;
int n,k,ansi;
long double nn,ln_k,n_e,ansd,pi=3.141592653589793,e=2.718281828459;
//每个数组或变量的含义详见处理过程。
in int qread()
//快读
{
int x=0,f=1;
char c;
c=getchar();
while(c<'0'||c>'9')
{
if(c=='-')
{
f=-1;
}
c=getchar();
}
while(c>='0'&&c<='9')
{
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}
in void qwrite(re int x)
//快写
{
if(x<0)
{
putchar('-');
x=-x;
qwrite(x);
}
else
{
if(x>9)
{
qwrite(x/10);
}
putchar(x%10+'0');
}
}
signed main()
{
n=qread();
k=qread();
//读入
ln_k=log(k);
//ln_k表示以e为底k的对数
if(n<=M)
//前50%的数据点:
{
for(re int i=2;i<=n;i+=2)
{
ansd+=log(i)/ln_k;
//ansd+=以k为底i的对数
}
ansi=ansd+eps+1;
//统计答案,这个eps真的非常重要
qwrite(ansi);
putchar('\n');
//输出答案
}
else
//后50%的测试点:
{
nn=(n>>1);
n_e=nn/e;
//n_e表示n/e的值
ansd=(log(2*pi*nn)*0.5+log(n_e)*nn)/ln_k;
//根据斯特林公式计算nn!并利用换底公式求以k为底nn!的对数
ansi=ansd+eps+1+log(2)/ln_k*nn;
//统计答案
qwrite(ansi);
putchar('\n');
//输出答案
}
return 0;
}
\(\ \ \ \ \ \ \)完美的一百分:
